Chaotic Waves for 3D Audio.

by Alastair Sibbald

3D audio synthesis is now widely used for interactive video games and in music processing. An initial feature of the synthesis is that the audio streams are convolved with Head-Related Transfer Functions (HRTFs), so as to simulate the acoustic processing which occurs naturally when sound waves arrive at the head and ears directly from the source. This alone, however, is an anechoic process, representing a rather unnatural environment which is free from all sound reflections and reverberation. In reality, a great deal of the sounds we hear are indirect sounds: they have been reflected and scattered.

Many attempts have been made to model and recreate the effects of room acoustics for 3D audio synthesis using known techniques such as ray or wave tracing methods and generic acoustic reverberation algorithms. However, although these can help create the effect of a particular acoustic environment, the headphone listener, unfortunately, perceives a sound image which is inside (or very close to) their own head.

In reality, the acoustic environments of rooms are not the simple ‘shoe box’ topographies that conventional models assume: they often include many complex-shape scattering objects and surfaces. Consequently, the listener is not subjected to a clean series of well-defined wall, ceiling and floor reflections, but a chaotic deluge of scattered and reflected elemental wavelets from a multitude of directions. These chaotic waves are the key to externalisation of the headphone image.

1 – Introduction

3D audio synthesis is now widely used for interactive video games and in music processing. An initial feature of the synthesis is that the audio streams are convolved with Head-Related Transfer Functions (HRTFs), so as to simulate the acoustic processing which occurs naturally when sound waves arrive at the head and ears directly from the source [1]. The audio is delivered to the listener, usually through a two-channel system, using either loudspeakers (in conjunction with transaural crosstalk cancellation [2,3]) or headphones.

The headphone listener, however, often finds the results less convincing because the sound image can appear to originate either inside, or close to, the head. For many years, attempts have been made to overcome this limitation and create the sonic illusion of a truly ‘external’ sound image.

The two principal approaches to this problem have been: (a) the incorporation of theoretically derived sound-wave reflections and room reverberation into the synthesis process; and (b) the acoustic measurement of a real room environment, in conjunction with considerable signal processing power (in the form of a convolution engine) to replicate the characteristics of that one, specific room. Neither of these methods has been entirely successful. The use of modelled reflections and reverberation can create the correct ‘sound’ of a room or acoustic environment successfully, but the sound image often lies very close to the listener’s head. The use of very lengthy convolution can create a much better external image, but the signal processing requirements are prohibitive for real­time interactive PC applications. In addition, they are fixed and static, and therefore unsuitable for interactive use.

This paper describes an advance in externalisation of the headphone image, in which the conventional models of room reverberation are set aside. Instead, it is recognised that the real-world irregularities which are present not only in rooms, but also in many outdoor environments, fragment and distribute the indirect waves which arrive at the ears of the listener, creating turbulent wave effects with chaotic properties. This phenomenon is the critical factor in externalisation of the headphone image.

A signal-processing engine has been developed to synthesise these ‘chaotic wave’ effects in real-time (referred to as the Sensaura Chaos Engine). This is now being integrated into Sensaura virtualizers and will soon be built into the 3D positional audio drivers. The technology can be used in conjunction with current 3D reverberation systems in order to provide both an external image and environmental effects simultaneously.

2 – Anechoic sounds, reflections and reverberation

The use of virtualization technologies for stereophonic applications is now well known [1,4], in which the objective is to create the aural illusion that the listener, using headphones, appears to hear a stereo sound source emanating from an invisible pair of ‘virtual’ loudspeakers in front of him or her. The present methodologies in use to achieve this are described below.

2.1 – Anechoic virtualisation

By measuring so-called ‘Head-Related Transfer Functions’ (HRTFs) from a sound source at specified locations in space, the spatially dependent acoustic processes which act on the incoming sound waves, caused by the head and outer ear, can be characterised. Each HRTF comprises three elements: (a) a left-ear transfer function; (b) a right-ear transfer function; and (c) an interaural time delay, and each is specific to a particular direction in three-dimensional space with respect to the listener.

Figure 1: HRTF processing

This data can be used to synthesise 3D audio electronically by convolving a monophonic sound source with a selected HRTF (Figure 1). The resultant two-channel signal contains the natural 3D sound cues which are introduced acoustically by the head and ears when we listen to sounds in real life, and include the interaural amplitude difference (IAD), interaural time difference (ITD) and spectral shaping by the outer ear. When the resultant stereo signal pair is introduced directly into the appropriate ears of the listener using headphones (or, alternatively, loudspeakers via transaural crosstalk cancellation processing), then he or she will perceive the original sound to be at a position in space in accordance with the spatial location of the HRTF pair which was used for the signal processing.

The effects can be quite remarkable. For example, it is possible to move the image of a sound source around the listener in a complete horizontal circle, beginning in front, moving around the right-hand side of the listener, behind the listener, and back around the left-hand side to the front again. It is also possible to make the sound source move in a vertical circle around the listener, and indeed make the sound appear to come from any selected position in space.

However, this method is anechoic (no sound wave reflections are present), and emulates listening to the sounds in an anechoic chamber. The consequent effect is that, although the direction of the sound source can be emulated reasonably well, its distance is very difficult to assess. For headphone users, the sound source appears to be situated very close to the head.

2.2 – Simulated reflections and reverberation

Figure 2: Conventional model of direct and indirect sound wave arrivals

It is well known that sound wave reflections and reverberation have a great influence on the perceived properties of sounds and that the ratio of direct sound (the wavefront which arrives at the listener by a direct path, without intervening reflection) to reverberant sound is a powerful influence on the perception of soundsource distance. A conventional depiction of the direct and reflected wave arrivals at the listener in a room is shown in Figure 2. The first wavefront to arrive (shown at t = 0) is the direct sound, followed several tens of milliseconds later by reflections from the four walls, ceiling and ground (usually within 30 ms). The reflected waves themselves then undergo further reflections (reverberation) which propagate and build up into a dense ‘reverb tail’. The indirect wave intensities decay exponentially, as shown, because the energy density of the ever expanding wavefront diminishes with an inverse square law characteristic. Additionally, the selective absorption of higher frequencies during propagation and reflection modifies the spectral properties somewhat, generally reducing the HF content of the signal with time. The reflection timing and decay properties, of course, are determined by the room size.

It is no surprise, then, that these effects have been incorporated into 3D audio synthesis in a variety of ways with the goal of providing a more authentic listening experience. An early example of this is described by Kendall and Martens [5], which describes a three dimensional audio processor intended primarily for headphone use, which incorporates spatial placement of the direct sound via HRTFs (‘pinna filtering’), together with both first- and second-order reflection groups and subsequent reverberation.

The magnitude and timing of sound reflections can readily be calculated for a hypothetical room, together with the associated reverberation. However, when these are incorporated into the virtualisation processing, then the externalisation of the headphone image is often improved a little, but nowhere near as much as might be expected from such careful calculation and application.

Even when great care is taken to adjust the reverberation parameters, it is difficult to achieve truly convincing ‘externalisation’ effects, even when using quite a complex reverberation engine (featuring all six accurately simulated first-order reflections, together with eight individual virtual reverberation sources). Although the resultant aural effects successfully create the ‘sound’ of the hypothetical room, the source itself, somewhat surprisingly, is not externalised properly. The results are not nearly so effective as might be expected by comparison, for example, with a live artificial head recording.

2.3 – Virtualization using room convolution (‘auralisation’)

The reverberation properties of a room or enclosed space can be measured in detail by means of an impulse method. This records the data represented in Figure 2 for a particular room by creating an impulse from a sound source and then measuring the resultant time-varying disturbance at another point, caused by the arrival of all the various direct and reflected wavefronts as a function of time.

By convolving the recorded impulse response onto an audio stream, the room characteristics can be reproduced accurately in the audio. If an artificial head is used as the means of recording the impulse, then the natural 3D hearing cues are integrated, too, for the particular relative positions of source and head in that one, particular acoustic situation.

However, this all requires quite a considerable computational resource because the reverberant effects might last several seconds. For example, if a room has a reverberation time of, say, four seconds (typical of a large recording studio), then the number of samples which must be recorded at a sample rate of 44.1 kHz is (4 x 44,100) = 176,400 samples. Bearing in mind that a typical, short HRTF requires 2 x 25 tap filters (50 samples total), then this 4-second room synthesis requires 3,528 times more computational effort! This is not practical using present consumer-type DSP technology. Furthermore, the room simulation would be only capable of emulating that one, particular room from which the measurements came. Also, note that twice this amount of processing would be needed for a two-channel system, such as a virtualiser.

By modelling the impulse responses of hypothetical rooms during the planning stage, it is possible for architects to listen to a sound synthesis of what the room will sound like before it has been built. This is commonly termed ‘auralisation’ and has application in the design of concert halls and theatres (although it can be fraught with errors).

This approach can often create convincing external sound images, attributed to the exhaustive complexity of the method. However, it is not a flexible simulation; it is the entire reproduction of one particular, fixed acoustic scenario. What is required is a method for creating an effective out-of-the-head sound image via headphones, which uses minimal (and practicable) signal processing power and which could be used in conjunction with different reverberation types.

3 – Acoustic wave tracing

The method of wave tracing has been used by acousticians for many years [5,6] to predict the progress of wave propagation in rooms and other acoustic spaces. The technique is more widely known in the context of optical ray tracing and is based on the same fundamental principle (Snell’s Law) that, for a reflected wave, the angle of reflection is equal to the angle of incidence. By applying this method to the expanding wavefront emitted from a sound source in a room, where it reflects from the boundaries, it is possible to ‘trace’ the arrival vectors of individual reflected waves as they arrive at the listener, using simple geometry. This is a very crude method of visualising the situation, but it has been adopted widely, perhaps because of its convenient synergy with reverberation modelling using delay lines, as described below.

Figure 3: Ray tracing method of locating virtual sound image

For example, Figure 3 shows the ray tracing method applied to a simple rectangular room, depicted here in plan view. The listener is placed in the centre of the room, for convenience, and there is a sound source to the front and on the right-hand side of the listener, at distance r, and at azimuth angle q. The room has width w, and length l. The sound from the source travels via a direct path to the listener, r, as shown, and also via a reflection off the right-hand wall such that the total path length is a + b. If the reflection path is extrapolated backwards from the listener and beyond the wall by its distance from the wall to the source, a, then this point specifies the position of the associated ‘virtual’ sound source. Because there is only a single reflection in the path from the source to listener, it is termed a ‘first-order’ reflection. There are six first-order reflections in all: one from each wall, one from the ceiling and one from the ground.

Geometric calculations yield the quantitative properties of the reflected waves (virtual position, distance, sound intensity and relative time delay), from which one can construct the actual positions of the first-order virtual sources. In the example shown here, the virtual source azimuth is given by the expression:

and its magnitude, V, as a fraction of that of the direct sound, is:

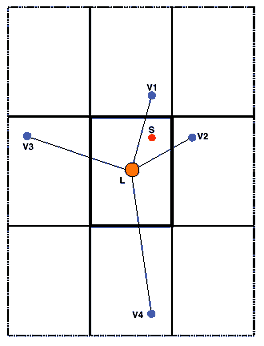
Figure 4: Image model showing adjacent virtual sources

By this means, the six first ­order virtual sources can be located (and also the higher orders). The four in­plane sources associated with Figure 3 are shown in Figure 4, overleaf. This philosophy of identifying virtual sources in a surrounding matrix of virtual rooms is known as the ‘image model’ [6]. However, as stated previously, the accurate simulation of the six first-order reflections makes surprisingly little difference to the effect or quality of the 3D audio image, either alone or with additional reverberation.

4 – Virtual rooms

Figure 5: Reverberator based on the image model

This approach to the modelling and simulation of room acoustics is widespread and lends itself to the use of reiterative delay-line methods for reverberation generation, as shown in Figure 5. Here, the delay line corresponds to the time taken for a sound wave to traverse a particular sized room and the feedback means incorporates an attenuator which corresponds to the sound wave intensity reduction caused by its additional distance of travel, coupled with reflection-related absorption losses. The upper series of diagrams in Figure 5 show the plan view of a room containing a listener and a sound source. The leftmost of these shows the direct sound path, r, and the first-order reflection from the listener’s right-hand wall (a + b). Hence, following the arrival of the direct sound at the listener (r ms after leaving the source), it can be seen that the additional time taken for the reflection to arrive at the listener corresponds to (a + b – r). The centre, upper diagram of Figure 5 shows this sound-wave progressing further to create a second-order reflection. By inspection, it can be seen that the additional path distance travelled is approximately one room width. The third, right-hand diagram in the series shows the wave continuing to propagate, creating a third-order reflection and here, by inspection, it can be seen that the wave has travelled about one additional room-width.

The lowermost diagram of Figure 5 shows a block schematic of a simple signal processing means, analogous to the above, to create a reverberant signal. The input signal passes through a first time delay {a + b – r} (which corresponds to the time-of-arrival difference between the direct sound and the first reflection), and an attenuator P, which corresponds to the signal reduction of the first-order reflection caused by its longer path-length and absorptive losses. This signal is fed to the summing output node and represents this one, particular, first-order reflection. It is also fed into another time delay element, w, corresponding to the room width, and attenuator Q, corresponding to the signal reduction per unit reflection (caused by additional distance travelled and absorptive losses). The resultant signal is also fed back to the summing node, which regenerates this latter process. Because of the successive delay-and-attenuate reiteration, the signal gradually decays to zero.

Figure 6: Reverberator output

The result of this delay line based reverberation method is depicted in Figure 6, which shows what the listener would hear. The first signal to arrive is the direct sound, with unit amplitude, followed by the first-order reflection (labelled ‘1’) after the ‘pre- delay’ time {a + b – r} and attenuated by a factor of P. Next, the second-order reflection arrives after a further time period of w, and further attenuation of Q (making its overall gain factor P*Q). The reiterative process continues ad infinitum, creating successive orders of simulated reflections 2, 3, 4… and so on, with decaying amplitude. By creating several delay line processing blocks according to Figure 5, each having different characteristics corresponding respectively to room width, height and length, it is possible to crosslink them for a more sophisticated reflections simulation.

In short, it is commonplace and convenient to model acoustic rooms and spaces using ‘shoe box’-type elements. This approach produces satisfactory results in the context of conventional stereo, but, unfortunately, it does not help significantly in the production of an external headphone image. Why is this so?

5 – Reality

Conventional methods of producing reflections and reverberation to externalise the headphone image fail because they are too simplistic. The analogous relationship between the image model and delay line reverberators steers our thinking away from the real-world situation. In reality, although rooms are, indeed, ‘shoe box’ in their construction, their interiors are usually filled with physical clutter that fragments and scatters the propagating wavefronts. This destroys the value of the image model and wave tracing for 3D-audio. In reality, the indirect waves that arrive at the listener are turbulent and chaotic in nature; they are not the ideal, discrete events as depicted in Figures 2 and 6.

The presence of physical features in a room, such as loudspeakers, chairs, equipment racks and so on, all scatter the sound waves from the sound source. Consequently, the listener receives first the direct sound (by definition), but this is followed quickly by a chaotic sequence of elemental contributions from the scattering objects, even before the first wall reflections arrive at the listener. It is this wave scattering which is the dominant feature in the 5 – 30 ms period. Following this, of course, the scattered waves themselves participate in the reflection and reverberation processes.

Figure 7: Modeled indirect sound arrivals (upper) vs. reality

This is shown in Figure 7, where all six first-order reflections have been calculated for a sound source in a 7 metre by 5 metre room, and plotted (uppermost) against a corresponding sound recording (lower). Although one can discern the first two reflections in the recording to arrive, at about 2.8 (ceiling) and 3.2 ms (ground), the remaining reflections are not present as they were anticipated. Instead, the recorded waveform has a turbulent nature with no distinct features other than a rapid onset and an exponential-type decay. This chaotic element is the key to headphone externalisation.

It is worth noting that this chaotic wave scattering occurs not only in rooms and reverberant spaces, but it is equally applicable to many outdoor scenarios. When one listens to sounds out of doors near to, for example, tables and chairs, foliage and the like, then it is quite easy to estimate the range of local sound sources, in the range, say, from 1 metre to 10 metres distance. It is much more difficult to do this in a ‘clear’ environment, such as in a field or on the beach. Similarly, an artificial head recording provides good externalisation in a ‘cluttered’ out-of-doors environment. Out-of-doors, of course, there are no room reflections or reverberation. It is the chaotic wave arrivals alone that provide the distance cue.

6 – Chaotic wave-scattering

Figure 8: Finite element model of wave propagation in 5 x 7 metre room depicting simple wave tracing (left) and chaotic wave scattering (right). (Elapsed times from top down: 2.2 ms; 4.2 ms; 7.4 ms; 10.4 ms)

The severe limitations of the wave tracing approach based on rectilinear geometry can be illustrated by comparing wave propagation in an empty room (on which the ‘image model’ is based) and a room containing several irregular objects. Figure 8, overleaf, shows a finite element model of a plan view of a 5 x 7 metre room in which a sound wave is propagating from a source in the upper left quadrant. The series on the left depicts the ‘image model’ scenario and the right series of images shows the chaotic wave arrivals owing to the small amount of acoustic clutter in the room. The scattering objects represent typical real-world objects in size, such as chairs and desks. Imagine that a listener is present in the centre of the room…

1: t = 2.2 ms

The first image pair (uppermost) corresponds to a time 2.2 ms after the impulse has been emitted from the source. The direct arrival is about to reach the listener in the centre.

2: t = 4.2 ms

At this stage, the wave has just reached the nearest wall to the source in the image model (left). However, already several scattering events have occurred in the chaotic system (right) and fragmented wavefronts are already propagating towards the listener.

3: t = 7.2 ms

The first reflection in the wave tracing scenario (left) has not yet reached the listener and the second reflection has only just begun to occur. In the chaotic wave room, the listener has already experienced multiple fragmented wave arrivals and the turbulent properties of the waves around him are increasing rapidly as the interactions multiply.

4: t = 10.4 ms

The listener has not yet experienced the second wave-traced reflection (left), but in the chaotic room, the scattering has already broken up most of the original wavefronts and the listener has experienced many fragmented wave arrivals.

It is interesting to note that when finite element models of this type are configured to produce a simple audio result (by sampling at two points about one head-width apart), then remarkable externalisation effects can be achieved. This is true even for very simple two-dimensional models, indicating the power of the phenomenon.

7 – Sensaura Chaotic Wave

Now that the key component for headphone externalisation has been identified, the next challenge is implementing the phenomenon effectively using practicable amounts of signal­ processing power.

Clearly, the scattered wave characteristics are dependent on many factors, primarily the size and spatial density of the scattering objects and their relationship to the source and listener. Also, a variety of options exist for defining the scattered wave properties, relating to how they are measured or modelled, and this will be the subject of a future white paper. (For example, the chaotic wave arrivals could be recorded using a free­field microphone or an artificial head microphone.)

Figure 9: Sensaura Chaotic Wave response (100 ms)

In the first instance, the chaotic wave properties of a 5 metre x 7 metre room have been chosen for use in Sensaura virtualisers and 3DPA drivers. These have been characterised and programmed into a specially developed signal-processing engine, referred to during its development as the Sensaura ‘Chaos Engine’. This generates the appropriate left-ear and right-ear chaotic wave phenomena from each audio input stream. The Chaos Engine requires relatively small amounts of signal processing power and generates a realistic chaotic impulse response as shown in Figures 9 and 10 (and comparable to that of the lower Figure 7). The primary application is for headphone listeners, because chaotic scattering is present naturally during loudspeaker listening.

Figure 10: Chaotic wave detail (35 ms)

Sensaura Chaotic Wave technology is complementary to all types of 3D reverberation systems and has already been integrated into Sensaura 3DPA as the headphone driver.

References:

Sibbald, Alastair, Hearing In 3 Dimensions, Sensaura Ltd., 2000.
Sibbald, Alastair, Transaural Acoustic Crosstalk Cancellation, Sensaura Ltd., 2000.
Sibbald, Alastair, Sensaura XTC Crosstalk Cancellation, Sensaura Ltd., 2000.
Sibbald, Alastair, Virtualization for Headphones, Sensaura Ltd., 1999.
Kendall, G.S. and Martens, W.L., Simulating the Cues of Spatial Hearing in Natural Environments, Proc. Int. Music Conf., 1984, pp. 111-125.
Allen, J.B. and Berkley, D.A., Image Method for Efficiently Simulating Small Room Acoustics, J. Acoust. Soc. Am., April 1979, pp. 943-950.

c. 2001, Sensaura Ltd.
From the Sensaura Ltd. website. Reproduced with permission.